概述

树状数组是支持 复杂度的维护和 的查询的数据结构，其本质是二叉树去掉了包含重复信息的节点而成的，即只保留了以下标为根的子树的所有信息，即 tree[n]保留以节点n为根的子树的和，形状如图：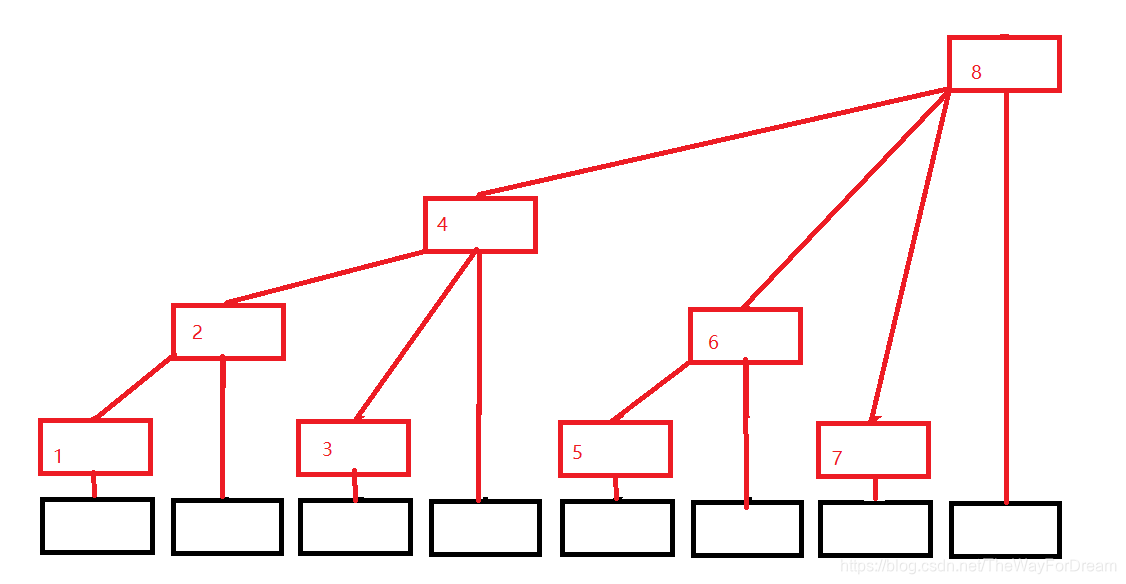

前置知识——lowbit的计算

对于一个数的二进制，例如 那么想要获得其最后的0的个数，可以利用补码的机制进行计算，即

1
2
3
4
int lowbit(int x)
{
 	return x & (-x);
}

这是由于，在计算机中，对于一个整形取相反数，就是各位取反然后末尾加1，那么末尾所有的0在取反的时候都会变成1，再+1之后，只有最后一个不是0的位会变成1，其余位都是0，而从最低有效位开始的第一个1之前的所有位都只会进行取反，而第二步+1的进位都影响不到，所以在按位与运算的时候都会变成0，只有第一个1的位置上面保留了1

关于树状数组结构的观察

观察上面那棵树的结构可以发现，每个节点下标的末尾有几个0就代表这个节点在第几层，例如1和3的末尾没有0所以在第0层，而8的二进制是1000末尾有三个0所以在第三层，那么可以知道，对于节点下标为的节点，包含了到这个区间的数的和 。而对于节点 它的父节点是

各类操作的实现

单点修改操作

单点修改操作主要就是通过不断加上当前的 来把所有包含了这个数的区间的节点全部加上对应的值，即：

1
2
3
4
5
int add(int pos, int val) {
	for (int i = pos; i <= n; i += lowbit(i)) {
		tree[i] += val;
	}
}

就实现了单点修改，这里的修改是把原数组的 pos 位置上面加上了 val 的值

对于 [0,r] 区间的求和

对于这种区间，可以发现，只需要不停地减去 lowbit(n) 就可以得到下一个未被覆盖的子区间的节点了，那么代码如下：

1
2
3
4
5
6
7
int inquiry(int right) {
	int sum = 0;
	for (int i = right; i > 0; i -= lowbit(i)) {
		sum += tree[i];	
	}
	return sum;
}

对于区间 [l,r] 的求和

不难发现：

那么就可以写出：

1
2
3
int inquiry_interval(int l, int r) {
	return inquiry(r) - inquiry(l - 1);
}

即可。